
Help / Documentation
This page describes the requirements, capabilities, and limitations of the current version of tex2solver. Please consult the user manual below if you are having system issues. These materials will be updated/refined/improved as tex2solver matures.
Table of Contents:
Overview
tex2solver converts linear programming (LP) or mixed integer linear programming (MILP) models from LaTeX code to Python solver code.
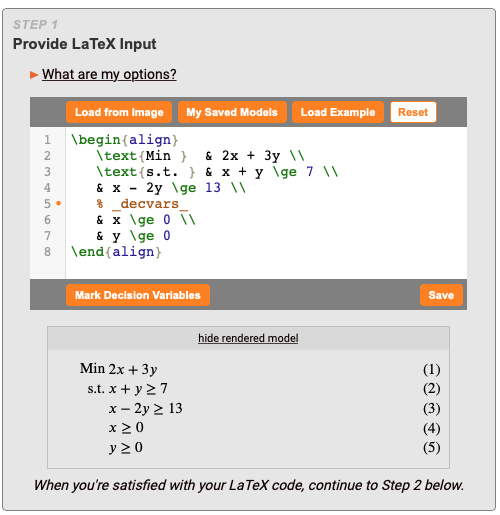
There are 4 ways to input an LP or MILP model:
- Paste directly from your LaTeX code. Click the "Load Example" button to view some sample code.
- Take a screenshot of a math model using the "Load from Image" button.
- From your smartphone, you can also use the "Load from Image" button to capture a picture of a math model.
- The MathPix Snip app is a third-party tool that converts images of mathematics to LaTeX code.
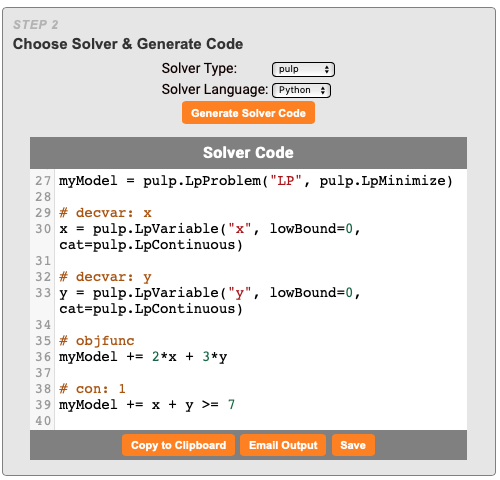
General Format -- Input
The input to tex2solver should be an LP or MILP formulation, consisting of an objective function, constraints, and decision variable definitions. This model should be written in LaTeX syntax. The image below depicts the five key elements of a model:

1 Math Environment
The model should be wrapped in any of the following environments:
\begin{align}and\end{align}\begin{flalign}and\end{flalign}\begin{array}and\end{array}\begin{gather}and\end{gather}\begin{equation}and\end{equation}\begin{eqnarray}and\end{eqnarray}
You may also use the "starred" versions of these environments (e.g., \begin{align*} and \end{align*}) to hide the equation numbers. This is purely cosmetic, and won't change the output code.
2 Objective Function
The first line of the formulation must be the objective function. This should start with any of the following, which indicate the "sense" of the objective (i.e., maximization or minimization):
\min\text{Min}\text{Minimize}\max\text{Max}\text{Maximize}
The "Min", "Minimize", "Max" and "Maximize" text strings are case insensitive. The \min and \max LaTeX tags are case sensitive.
The objective function should end with two backslashes (\\). For example:
| LaTeX Code | Rendered | |
|---|---|---|
\text{Min } 2x + 3y \\
| \(\text{Min } 2x + 3y \) |
3 Constraints
The first constraint should appear on the next line after the objective function. This constraint should begin with one of the following LaTeX tags:
\text{subject to}\text{such that}\text{s.t.}
The "subject to", "such that" and "s.t." text strings are case insensitive.
Subsequent constraints should not start with a "subject to" tag (i.e., your model should have exactly one "subject to" tag).
Each constraint should end with two backslashes (\\). For example:
| LaTeX Code | Rendered | |
|---|---|---|
\text{s.t. } & x + y \ge 7 \\
& x - 2y \ge 13 \\
| $$ \begin{align*} \text{s.t. } & x + y \ge 7 \\ & x - 2y \ge 13 \\ \end{align*} $$ |
4 Decision Variable Flag
Decision variable definitions should appear after the constraints. The block of decision variable definitions must begin with the following LaTeX comment:
% _decvars_- The "decvars" text is case insensitive.
- An arbitrary number of spaces are allowed after the
%symbol.
tex2solver will warn you if you forget to include this flag. The "Mark Decision Variables" button will help you place this flag in your model.

5 Decision Variable Definitions
To generate usable solver code, tex2solver needs to know which elements of your model are decision variables. Thus, each decision variable should be explicitly defined after the % _decvars_ line.
Each decision variable definition should end with two backslashes (\\). For example:
| LaTeX Code | Rendered | |
|---|---|---|
% _decvars_ x \ge 0 \\ y \ge 0 \\ | $$ \begin{align*} & x \ge 0 \\ & y \ge 0 \end{align*} $$ |
In this document we will use the following terms:
- "decision variable": This phrase explicitly refers only to decision variables. Decision variables are the unknowns in your LP or MILP model (i.e., the stuff you want the solver to find).
- The solver will need to know which parts of your model are decision variables. tex2solver uses the
% _decars_line so it can pass this information along to the solver.
- The solver will need to know which parts of your model are decision variables. tex2solver uses the
- "parameter": This is a known value, and will be an input to your IP/MILP model. This could be a scalar (e.g., \(s = 3.2\)), it could be a set (e.g., \(I = [1, 2, 3, 4]\)), or some more complicated data structure (e.g., \(\Phi_q^t\) could represent a specific value from a 2-dimensional array named \(\Phi\)).
- You will be responsible for editing the Python code to provide numeric values for all of the parameters. For example, if your LP model uses \(Q\) to represent some set of values, you'll need to let Python know what values are actually contained in
Q.
- You will be responsible for editing the Python code to provide numeric values for all of the parameters. For example, if your LP model uses \(Q\) to represent some set of values, you'll need to let Python know what values are actually contained in
- "variable": We will use this generic term to describe both "decision variables" and "parameters". It may be helpful to think of "variable" in the context of computer programming (where things that can be assigned a value are called variables), rather than in the context of linear programming. By using the term "variable", we won't have to write the longer phrase "decision variable or parameter" so often.
LaTeX Math Model Details
This section covers the expected LaTeX math syntax of a mathematical model and how it is interpreted. This includes what is supported in terms of notation, decision variable definitions, summations, and "forall" statements.
Before we continue, let's introduce tex2solver's terminology for describing parameter and decision variable notation. We'll do this using the example of \hat{x}^{ab}_{\sigma,c}:
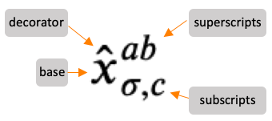
- The "base" of this notation (which could represent a parameter or a decision variable) is
x. - "Decorators" can be used to augment the base. In this case, the
\hatis a decorator. - Subscripts and superscripts can be used to represent indices. They can also be used to augment the base.
Keep reading below for more details...but keep in mind these two very important things:

Parameters and decision variables are restricted to a base with a single character.
xis acceptable.\alphais acceptable, because it is interpreted as being the single Greek letter \(\alpha\).xyis not acceptable. It will be interpreted asx*y\text{cost}is not currently acceptable as a "base" because it is a text string.

Each index is also restricted to single characters. See examples below.
Indices
Indices of decision variables and parameters can be set as either subscripts (using the underscore,
_) or superscripts (using the^symbol). Note that each character inside the braces will be considered individually. For example, if the subscript consists ofij, tex2solver will treat this as separate charactersiandj.Indices vs. Name Modifiers
tex2solver applies some rather specific rules to translate variable notation from LaTeX to Python. Subscripts and superscripts that are indices of a variable are converted as keys of a dictionary associated with the "base" variable. Non-indices are converted as part of the variable name separated by an underscore (
_).The key issue is whether the contents in the subscripts and superscripts should be part of the variable name itself, or indices.
Let's start with the easy stuff.
- The following items will always augment the base:
- Decorators. See here for a list of all decorators supported by tex2solver.
- Primes (which are really just a special kind of decorator)
- Certain specific items that can appear in subscripts or superscripts:
- Anything in a
\text{}tag; - The
+,-, or*symbols, if they are not being used to perform a mathematical operation; and - The
\minand\maxtags.
- Anything in a
xis augmented. There are no indices in these examples.
LaTeX Input Rendered Python Output a decorator \hat{x}\(\hat{x}\) x_hatdouble prime x''\(x''\) x_dprimea text label x^{\text{alt}}\(x^{\text{alt}}\) x_altarithmetic symbol x_{+}\(x_{+}\) x_plusmin tag x_{\min}\(x_{\min}\) x_mincombination x_{*}^{\max}\(x_{*}^{\max}\) x_star_max
Now, suppose we have a defined a decision variable named
x_{i}(\(x_i\)). Should this become an indexed data structure in Python (e.g.,x[i]) or shouldiaugment the base variable (e.g.,x_i)? It depends on exactly how the decision variable was defined.- If the variable was defined simply as
x_i \ge 0(\(x_i \ge 0\)), then the Python output is a single scalar variable namedx_i. - If the variable was defined as
x_i \ge 0 \forall i \in I(\(x_i \ge 0 ~ \forall ~ i \in I\)), then the Python output will treatxas an indexed data structure:x[i].
What if there are multiple entries in a super/subscript? Will these be treated as indices or as modifiers of the base variable name? The answer, again, is "it depends". However, now there's another factor to consider: The presence of a comma
At some point (hopefully soon) we'll document all of the detailed rules. In the meantime, please consult the following examples.,.- If none of the entries in a given superscript or subscript (in this case,
i,j, andk) are also specified in the associated "forall" statement, then the entries will augment the base (in this case,x):LaTeX Input Python Output x_{ijk}(\(x_{ijk}\))becomes x_i_j_kx_{i,j,k}(\(x_{i,j,k}\))becomes x_i_j_kx_{i jk}(\(x_{i jk}\))becomes x_i_j_kx_{ij,k}(\(x_{ij,k}\))becomes x_ij_k - If any of the entries in a given superscript or subscript are also specified in the associated "forall" statement, then the entries will become indices:
LaTeX Input Python Output x_{ijk}(\(x_{ijk}\))becomes x[i][j][k]x_{i,j,k}(\(x_{i,j,k}\))becomes x[i][j][k]x_{i jk}(\(x_{i jk}\))becomes x[i][j][k]x_{ij,k}(\(x_{ij,k}\))becomes x[i*j][k]
- The following items will always augment the base:
Single index
If a decision variable or parameter has one index as a single subscript or superscript, the argument does not have to be wrapped inside braces
{ }. The following are allowable:x_iis equivalent tox_{i}, and both are rendered as \(x_{i}\). The Python representation will bex[i].x^\alphais equivalent tox^{\alpha}, and both are rendered as \(x^{\alpha}\). The Python representation will bex[alpha]x_i^jis equivalent tox_{i}^{j}, and both are rendered as \(x_i^j\). The Python representation will bex[i][j].

If both subscripts and superscripts are used, subscripts are given precedence. For example,
x_i^jandx^j_iwill be represented in Python asx[i][j].Multiple indices
If a decision variable or parameter has multiple indices described in subscripts or superscripts, the arguments must be wrapped inside braces
{ }. The individual indices can be separated by commas, spaces, or not separated at all. For example:x_{i,j}is rendered as \(x_{i,j}\).
xis the "base", andiandjare considered to be the two indices ofx. The Python representation will bex[i][j].x_{i j}is rendered as \(x_{i j}\).
Again,xis the "base", andiandjare considered to be the two indices ofx. The Python representation will bex[i][j], which is the same as if we had definedx_{i,j}with a comma separating the subscripts.y^{ijk}is rendered as \(y^{ijk}\).
The Python representation will have 3 indices:y[i][j][k].

Note what happens if we forget to wrap multiple indices inside braces:
x^ijkis rendered as \(x^ijk\) (indices \(j\) and \(k\) are not included in the superscript). The Python code will becomex[i]*j*k.Nested subscripts/superscripts
Nesting subscripts and superscripts is allowed, but only to modify the naming of an index or indices.
x_{i_\alpha}is rendered as \(x_{i_\alpha}\).
In Python, this will be represented asx[i_alpha], wherexis the name of the data structure (the "base") andi_alphais the index.x_{i^+}is rendered as \(x_{i^+}\).
In Python, this will bex[i_plus].x^{i^{\alpha}j}is rendered as \(x^{i^{\alpha}j}\).
In Python, this will become a 2-index variable:x[i_alpha][j]
Decision Variables
All decision variables must be defined after the
% _decvars_comment in LaTeX. There should be no constraints after that comment.In general, decision variables are defined in individual lines of the model. For example:
x \ge 0 \\ y \in \{0, 1\}However, it is possible to "overload" decision variable definitions, as in:
x_{i}, y_{i} \geq 0 \forall i \in IOverloading of decision variable definitions is only permissible if:
- The variables have the same bounds (e.g.,
\geq 0), and - The variables share the same "forall" conditions (e.g.,
\forall i \in I).
Continuous non-negative decision variables
In a single-bounded definition, the first value must be the decision variable, followed by a relational comparator and then a parameter. The parameter can be a number, a variable without indices, or a variable with indices. For example:
p \ge 30(\(p \ge 30\))q \le b(\(q \le b\))r \le \hat{c}(\(r \le \hat{c}\))s_i \le d_i \forall i \in I(\(s_i \le d_i ~ \forall ~ i \in I\))

tex2solver currently supports only non-negative decision variables. If the relational comparator is
\le, then the decision variable is also assumed to be\ge 0.In a double-bounded definition, the middle value between relational comparators must be the decision variable. For example:
0 \le x \le 1(\(0 \le x \le 1\))

The default decision variable type is "continuous". You don't need to explicitly declare a variable to be continuous-valued.
Integer Decision Variables
Integer decision variables can be defined using any of the following LaTeX syntax:
\ge 0 \text{ and integer }(rendered as \(\ge 0 \text{ and integer }\));\in \mathbb{Z}(rendered as \(\in \mathbb{Z}\));\in \mathbb{Z}^{+}(rendered as \(\in \mathbb{Z}^{+}\));\in \mathcal{Z}(rendered as \(\in \mathcal{Z}\)); or\in \mathcal{Z}^{+}(rendered as \(\in \mathcal{Z}^{+}\)).
For example:
x_i >= \alpha \text{ and integer} c_{ijk} \in \mathcal{Z}
Any LaTeX text commands used to describe the type of decision variable must only come immediately before the
\foralltag (if applicable) or at the end of the line (if there's no\foralltag). For example:x_i \ge 0 \text{ and integer } \forall i \in I
\(x_i \ge 0 \text{ and integer } \forall i \in I\)y \ge 0 \text{ and integer}
\(y \ge 0 \text{ and integer}\)
Binary Decision Variables
Define binary decision using:
\in \{0, 1\}(rendered as \(\in \{0, 1\}\)) or\ge 0 \text{ and binary }(rendered as \(\ge 0 \text{ and binary }\)).

Matching "escaped" braces (
\{and\}) are the preferred way of defining ranges or collections of values. Non-escaped braces won't actually display when rendered:\in {0,1}is rendered as \(\in {0, 1}\).
- The variables have the same bounds (e.g.,
Set definitions and operations
Sets may be defined as collections of individual values, ranges, or parameters. For example:
\{0, 3, 6, 10\}(\(\{0, 3, 6, 10\}\)) represents a collection of values;\{2, 5, \ldots, n\}(\(\{2, 5, \ldots, n\}\)) represents a range of values from 2 thru \(n\) in increments of 3; and- Parameter
Icould represent a set.

You may use
\ldots(\(\ldots\)),\cdots(\(\cdots\)), or three periods...to indicate a range.- If you provide three values in the range (e.g.,
\{2, 5, \ldots, n\}), the difference between the second value and the first will be used to determine the step size. - If you only provide two values in the range (e.g.,
\{2, \ldots, 5\}), the step size will be assumed to be 1.

Python's range operator uses the form
range(start, stop, [step]), where the start value equalsstartand the end value is up to but not includingstop. For this reason, the Python translation of\{1, 2, \ldots, n\}isrange(1, n+1)(rather thanrange(1, n)). The step size is optional. Each of the values must be integers.
Matching "escaped" braces (
\{and\}) are the preferred way of defining ranges or collections of values. Non-escaped braces won't actually display when rendered:\in {0,1}is rendered as \(\in {0, 1}\).Supported set operators:
\in(\(\in\))\notin(\(\notin\))\cup(\(\cup\)) or\bigcup(\(\bigcup\)) represent set union\cap(\(\cap\)) or\bigcap(\(\bigcap\)) represent set intersection\setminus(\(\setminus\)) is used to exclude one or more items from a set
Conditionals
Conditionals are represented by a colon
:, meaning "such that".i \in \{A : i \ne j\}i \in \{A : i \leq j\}
Conditionals may be applied within
\forallstatements and summations.Absolute Value vs. Set Cardinality vs. Conditionals
tex2solver applies several rules to differentiate among absolute value, cardinality of a set, and a conditional expression. There are many different ways to convey these three mathematical constructs in LaTeX; the trick is in translating this to the correct solver code.
The list below provides a guide for choosing the LaTeX symbols that will result in solver code that does what you actually intended.
- If you want to find the absolute value of an expression, use:
\abs{}- For example, the absolute value of the difference between two scalars
aandbwould be written in LaTeX as\abs{a - b}(rendered as \(|a - b|\)).
- If you want to reference the cardinality of a set, there are several options:
- Use two
|(pipe) symbols. For example, the number of elements in setSwould be| S |(rendered as \(| S |\)). - Use two
\verttags, which also produce the pipe symbol in LaTeX. For example,\vert S \vert(rendered as \(\vert S \vert\)). - Use
\lvertand\rverttags to produce the pipe symbols in LaTeX. For example,\lvert S \rvert(rendered as \(\lvert S \rvert\)).
- Use two
- If you want to apply a condition to a set, use:
:- For example, if you want to consider all elements
jof a setJsuch thatjis not equal to some scalari, write:\forall j \in \{J : j \ne i\}, which is rendered as \(\forall j \in \{J : j \ne i\}\).

The conditional symbol (
:) cannot appear within escaped braces (\{and\}) if set cardinality is also used within those braces. For example,\forall j \in \{1, \ldots, |N| : j \ne i\}will cause an error. Instead, write this as\forall j \in \{1, \ldots, |N|\} : j \ne i.There are several tags that are not supported by tex2solver. These include:
\mid,\norm{}, and\|(an "escaped" pipe symbol, which actually produces double pipes).
If none of these options work for you, please email us with an explanation of your use case.
- If you want to find the absolute value of an expression, use:
Forall statements
The
\forall(\(\forall\)) tag may be used in constraints and decision variable definitions (i.e., it cannot be used in the objective function).When there are multiple indices that need to be defined in a
\forallstatement, make sure the definitions are separated by a comma. For example:x_{i,j} \geq 0 \forall i \in A, j \in B
tex2solver supports "overloaded"
\forallstatements, which can simplify notation. For example:x_{i,j} \ge 0 \forall i \in A, j \in Acan be re-written as
x_{i,j} \ge 0 \forall i, j \in A.
Summations
The
\sum(\(\sum\)) tag may be used in the objective function and constraints (i.e., it cannot be used to define indices in the decision variable definitions).Index definition
Subscripts and superscripts are also applied to summations to define the index space. The index can be defined by setting lower and upper limits or by specifying a set. For example:
\sum_{i=0}^n(\(\sum_{i=0}^n\))\sum_{i \in I}(\(\sum_{i \in I}\))
Conditionals inside the subscripts using the colon qualifier are also supported. For example:
\sum_{i \in \{A : i \neq j\}}(\(\sum_{i \in \{A : i \neq j\}}\))
Wrapping summation terms
The terms associated with a summation must be wrapped by the following bracket types:
( )\( \)\{ \}\leftand\rightmay be applied to the brackets
The terms of a summation should be wrapped to avoid any ambiguity of when the summation ends. For example, consider the
\sum_{i=0}^n x_i+y_i - z(\(\sum_{i=0}^n x_i+y_i - z\)).- If
x_j+y_ibelong inside the summation, but the subtraction ofzdoes not, thex_j+y_ishould be wrapped using the suggested brackets:\sum_{i=0}^n \{x_i+y_i\} - z(\(\sum_{i=0}^n \{x_i+y_i\} - z\)).
In the case of nested summations, the terms at the deepest level should be wrapped inside the supported bracket types. The nested
\sumcommand and its index definition do not have to be wrapped. For example:\sum_{i=0}^n \sum_{j=0}^n \{X_i+y_i\} - z(\(\sum_{i=0}^n \sum_{j=0}^n \{X_i+y_i\} - z\)).
Substacks
The
\substack{}command allows stacking of multiple lines in the subscript of a summation. This command can be used to specify the index space as a set relation, inequality, or equation. Lines should be separated by\\. For example:\sum_{\substack{i=0 \\ i \neq j}}^n(\(\sum_{\substack{i=0 \\ i \neq j}}^n\))

Use of the colon qualifier (
:) to specify a conditional is not currently supported inside a\substack{}tag. For example,\sum_{\substack{i \in \{A : i \neq j\}}}(\(\sum_{\substack{i \in \{A : i \neq j\}}}\)) will currently produce an error.Overloaded summations
It is possible to "overload" a single summation with multiple indices. For example:
\sum_{i,j \in Q} x_{ij} \ge 0(\(\sum_{i,j \in Q} x_{ij} \ge 0\)).
Horizontal spacing
Horizontal spacings are commonly used to separate a constraint or decision variable definition and their forall statement. For example:
| Using Spacing Tags | Without Spacing | |
|---|---|---|
x_i \ge 0 \quad \forall ~ i \in I |
x_i \ge 0 \forall i \in I |
|
| $$x_i \ge 0 \quad \forall ~ i \in I$$ | $$x_i \ge 0 \forall i \in I$$ |
Currently, tex2solver supports the following horizontal space tags: \quad, \qquad, ~, \enspace, \hspace{}, and \thinspace.
The use of these tags is for purely cosmetic purposes. Spacing does not change the generated solver code.
Greek Letters
Greek letters can be used as decision variables, parameters, or to modify the names of variables and parameters.
The following is a list of Greek letters in LaTeX and their conversion in the output solver code.
| LaTeX | Python | LaTeX | Python | |||
|---|---|---|---|---|---|---|
| \(\alpha\) | \alpha | alpha | ||||
| \(\beta\) | \beta | beta | ||||
| \(\gamma\) | \gamma | gamma | \(\Gamma\) | \Gamma | Gamma | |
| \(\delta\) | \delta | delta | \(\Delta\) | \Delta | Delta | |
| \(\epsilon\) | \epsilon | epsilon | ||||
| \(\varepsilon\) | \varepsilon | varepsilon | ||||
| \(\zeta\) | \zeta | zeta | ||||
| \(\eta\) | \eta | eta | ||||
| \(\theta\) | \theta | theta | \(\Theta\) | \Theta | Theta | |
| \(\vartheta\) | \vartheta | vartheta | ||||
| \(\iota\) | \iota | iota | ||||
| \(\kappa\) | \kappa | kappa | ||||
| \(\lambda\) | \lambda | lmbda* | \(\Lambda\) | \Lambda | Lmbda* | |
| \(\mu\) | \mu | mu | ||||
| \(\nu\) | \nu | nu | ||||
| \(\xi\) | \xi | xi | \(\Xi\) | \Xi | Xi | |
| \(\pi\) | \pi | pi | \(\Pi\) | \Pi | Pi | |
| \(\varpi\) | \varpi | varpi | ||||
| \(\rho\) | \rho | rho | ||||
| \(\varrho\) | \varrho | varrho | ||||
| \(\sigma\) | \sigma | sigma | \(\Sigma\) | \Sigma | Sigma | |
| \(\varsigma\) | \varsigma | varsigma | ||||
| \(\tau\) | \tau | tau | ||||
| \(\upsilon\) | \upsilon | upsilon | \(\Upsilon\) | \Upsilon | Upsilon | |
| \(\phi\) | \phi | phi | \(\Phi\) | \Phi | Phi | |
| \(\varphi\) | \varphi | varphi | ||||
| \(\chi\) | \chi | chi | ||||
| \(\psi\) | \psi | psi | \(\Psi\) | \Psi | Psi | |
| \(\omega\) | \omega | omega | \(\Omega\) | \Omega | Omega |
* lambda is a reserved keyword in Python. The LaTeX \lambda tag is intentionally written in Python without the first "a" (as in lmbda). For consistency, the upper case \Lambda is similarly written in Python as Lmbda.
Decorators
Decorators can be used to modify the name of a variable or parameter.
The following is a list of decorators in LaTeX, applied to variablex, and how they are converted to solver code.
| LaTeX Decorator | Variable Name | |
|---|---|---|
| \(x'\) | x' | x_prime |
| \(x''\) | x'' | x_dprime |
| \(x'''\) | x''' | x_tprime |
| \(\acute{x}\) | \acute{x} | x_acute |
| \(\bar{x}\) | \bar{x} | x_bar |
| \(\breve{x}\) | \breve{x} | x_breve |
| \(\check{x}\) | \check{x} | x_check |
| \(\dot{x}\) | \dot{x} | x_dot |
| \(\ddot{x}\) | \ddot{x} | x_ddot |
| \(\dddot{x}\) | \dddot{x} | x_dddot |
| \(\grave{x}\) | \grave{x} | x_grave |
| \(\hat{x}\) | \hat{x} | x_hat |
| \(\widehat{x}\) | \widehat{x} | x_widehat |
| \(\mathring{x}\) | \mathring{x} | x_mathring |
| \(\overline{x}\) | \overline{x} | x_overline |
| \(\underline{x}\) | \underline{x} | x_underline |
| \(\overbrace{x}\) | \overbrace{x} | x_overbrace |
| \(\underbrace{x}\) | \underbrace{x} | x_underbrace |
| \(\tilde{x}\) | \tilde{x} | x_tilde |
| \(\widetilde{x}\) | \widetilde{x} | x_widetilde |
| \(\vec{x}\) | \vec{x} | x_vec |

Decorators may only be applied to single symbol arguments.
| Allowed | Not Allowed | |||
|---|---|---|---|---|
| \(\grave{x}\) | \grave{x} | \(\grave{xy}\) | \grave{xy} | |
| \(\tilde{\alpha}\) | \tilde{\alpha} | \(\tilde{\alpha\beta}\) | \tilde{\alpha\beta} | |
| \(\vec{x}_i\) | \vec{x}_i | \(\vec{x_i}\) | \vec{x_i} | |
PuLP Solver Options
PuLP provides several options for choosing a solver. By default, tex2solver assumes the use of the solver that is packaged with PuLP. However, one of the powerful features of PuLP is that it allows the user to choose from several different solvers. Details on available solvers may be found in the PuLP documentation at https://coin-or.github.io/pulp/technical/solvers.html.



